Fibonacci

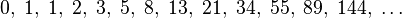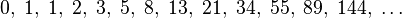Fibonacci sequence is a series in the following sequence                                                          It can be easily seen from the above sequence that it is following this recurrence relation :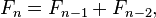

    

Making a program of Fibonacci series is really easy. Here we will discuss to make Fibonacci series using iterative method and recursion.

Iterative Method

In this method we simply store the previous two values in two variables and use

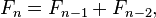  to calculate next value.

Recursive Method

We normally do not use recursion to find Fibonacci numbers because if we do so, we calculate each value again and again.

function fib(n)
       if n <=1 return n
       return fib(n − 1) + fib(n − 2) 

Notice that if we call, say, fib(5), we produce a call tree that calls the function on the same value many different times:

1. fib(5)
2. fib(4) + fib(3)
3. (fib(3) + fib(2)) + (fib(2) + fib(1))
4. ((fib(2) + fib(1)) + (fib(1) + fib(0))) + ((fib(1) + fib(0)) + fib(1))
5. (((fib(1) + fib(0)) + fib(1)) + (fib(1) + fib(0))) + ((fib(1) + fib(0)) + fib(1))

Finding same values again and again is not a good option. Therefore we do not use recursion.
Here is the program using recursion

Read More

QuickSort

Defination

Quicksort, or partition-exchange sort, is a sorting algorithm which follows divide and conquer algorithm. We will first study the algorithm 

then will implement the algorithm in a C++ program.

Algorithm

Quicksort first divides a large array into two smaller sub-arrays: the low elements and the high elements. Quicksort can then recursively sort the sub-arrays.
The steps are:

1. Pick an element, called a pivot, from the array.
2. Reorder the array so that all elements with values less than the pivot come before the pivot, while all elements with values greater than the pivot come after it (equal values can go either way). After this partitioning, the pivot is in its final position. This is called the partition operation.
3. Recursively apply the above steps to the sub-array of elements with smaller values and separately to the sub-array of elements with greater values. 

Recursion

In the quicksort function we pass the array and quicksort sorts elements i through k (inclusive) of array A. Then we check if left is less than right. If it is true we call partition. The partition array returns us a pivot index in the array, and the array is also changed.
Now the elements on the left hand side is smaller than the value of the pivot index and the elements on right side are larger than the pivot index.

We now call the quicksort function again but now for the smaller array of left hand side of the pivot index and similarly for the array on the right hand side of the pivot. These calls are made recursively.

 quicksort(A, i, k):
  if i < k:
    p := partition(A, i, k)
    quicksort(A, i, p - 1)
    quicksort(A, p + 1, k)

 Partition    

This is the in-place partition algorithm. It partitions the portion of the array between indexes left and right, inclusively, by moving all elements less than or equal array[pivotIndex] before the pivot, and the greater elements after it.We have used last element of the array as pivot index. We compare every element of the array with the pivot index and if it is less than pivot, we swap it with array[storeIndex]. Elements with indexes less than storeIndex are less than pivot. Notice that an element may be exchanged multiple times before reaching its final place. Also, in case of pivot duplicates in the input array, they can be spread across the right subarray

  // left is the index of the leftmost element of the subarray
  // right is the index of the rightmost element of the subarray (inclusive)
  // number of elements in subarray = right-left+1
  partition(array, left, right)
     pivotIndex := array[right]
     pivotValue := array[pivotIndex]
     swap array[pivotIndex] and array[right]
     storeIndex := left
     for i from left to right - 1
         if array[i] < pivotValue
             swap array[i] and array[storeIndex]
             storeIndex := storeIndex + 1
     swap array[storeIndex] and array[right] 

      // Move pivot to its final place
     return storeIndex 

 

Program

This is implementation of quicksort in C++.

Here is Scarlett Johansson if u didn't understand anything above. I hope it will make u feel better :)

Read More